Binary vs. Binary (unpaired/independent)
Test
Perhaps the most commonly used test when you have two binary variables is the Fisher (Exact) Test (Fisher, 1922). It tests if "the relative proportions of one variable are independent of the second variable; in other words, the proportions at one variable are the same for different values of the second variable" (McDonald, 2014, p. 77)
In the example with gender and secondary school, the Fisher test will produce a significance (p-value) of 0.298844. This indicates that there is a probability of 0.2988 to have a result as in our sample, or even more extreme (rare) if the assumptions that they are independent is true. Usually, if this value is below 0.05 we would reject the assumption and conclude that there is a significant association. In this example, it is above .05 so no evidence to reject the assumption. So, no evidence to suggest the gender had an association with the location of the secondary school.
Click here to see how to perform Fisher's Exact Test...
with Flowgorithm
A flowgorithm for Fisher's Exact Test in Figure 1.
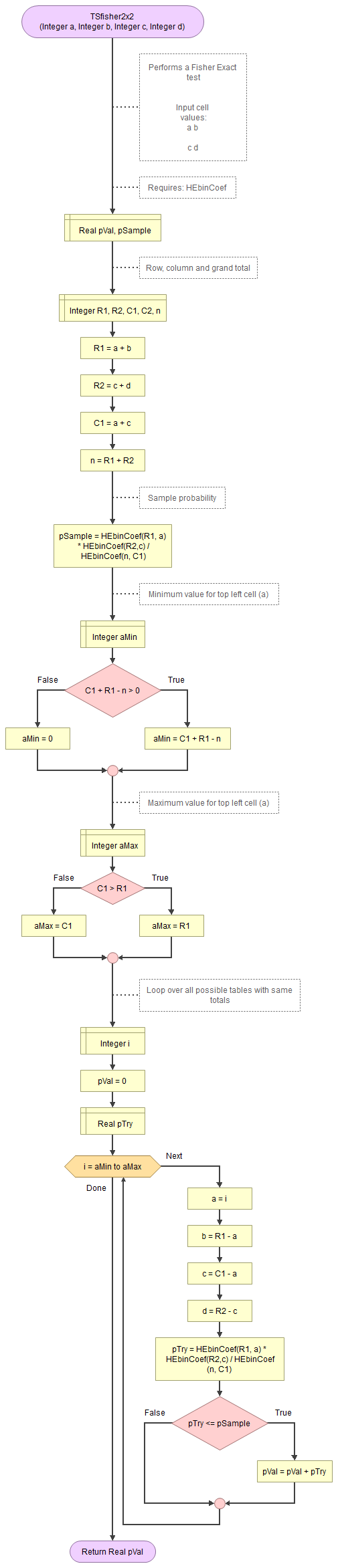
It takes as input paramaters four counts (one for each cell).
It uses a function the binomial coefficient.
Flowgorithm file: FL-TSfisher2x2.fprg.
with Python
video to be uploaded
Jupyter Notebook: TS - Fisher Exact (2x2).ipynb.
Data file: StudentStatistics.csv.
with R (Studio)
video to be uploaded
R script: TS - Fisher Exact (2x2).R.
Data file: StudentStatistics.csv.
with SPSS
video to be uploaded
manually (formula and example)
If we are given a 2 by 2 table, and label each cell as shown in Table 1.
| Col. 1 | Col. 2 | Total | |
|---|---|---|---|
| Row 1 | a |
b |
R1 = a + b |
| Row 2 | c |
d |
R2 = c + d |
| Total | C1 = a + c |
C2 = b + d |
n = R1 + R2 |
We can then use the following algorithm:
Step 1: Determine the probability of the sample table.
\(p_{sample} = \frac{\binom{R1}{a}\times\binom{R2}{c}}{\binom{n}{C1}} = \frac{\binom{R1}{b}\times\binom{R2}{d}}{\binom{n}{C2}}\)
This formula uses the binomial coefficient, defined as:
\(\binom{x}{y}=\frac{x!}{y!\times\left(x-y\right)!}\)
Which in turn uses the factorial operator (!), defined as:
\(x! = \prod_{i=1}^x i\)
Step 2: Determine the minimum and maximum of the top-left cell.
\(a_{min} = \text{MAX}\left(0, C1 + R1 - n\right)\)
\(a_{max} = \text{MIN}\left(R1, C1\right)\)
The reason for the minimum value of 'a', is first that it cannot be negative, since these are counts. So 0 would be the lowest ever possible. However, once 'a' is set, and the totals are fixed, all other values should also be positive (or zero). The value for 'b' will be if 'a' is 0, it will simply be R1 - a. The value for 'c' is also no issue, this is simply C1 - a. However 'd' might be negative, even if a = 0. The value for 'd' is n - R1 - c. Since c = C1 - a, we get d = n - R1 - C1 + a. But this could be negative if R1 + C1 > n. So, 'a' must be at least C1 + R1 - n.
The maximum for 'a' is simply the minimum of either it's row total, or column total.
Step 3: Go over all possible values of the top-left cell and calculate the probability. Add it to the p-value if it is less or equal to the one from the sample.
Worked out example
We'll use the example used earlier, shown in Table 2.
| Col. 1 | Col. 2 | Total | |
|---|---|---|---|
| Row 1 | a = 8 |
b = 16 |
R1 = 24 |
| Row 2 | c = 3 |
d = 15 |
R2 = 18 |
| Total | C1 = 11 |
C2 = 31 |
n = 42 |
Step 1: Determine the probability of the sample table.
Filling out the formula we get:
\(p_{sample} = \frac{\binom{24}{8}\times\binom{18}{15}}{\binom{42}{11}}\)
Using the formula for the binomial coefficient:
\(p_{sample} = \frac{\frac{24!}{8!\times\left(24-8\right)!}\times\frac{18!}{15!\times\left(18-15\right)!}}{\frac{42!}{11!\times\left(42-11\right)!}}\)
\( = \frac{\frac{24!}{8!\times16!}\times\frac{18!}{15!\times3!}}{\frac{42!}{11!\times31!}}\)
\( = \frac{\frac{24\times23\times\dots\times17}{8!} \times \frac{18\times17\times16}{3!}}{\frac{42\times41\times\dots\times32}{11!}}\)
\( = \frac{\frac{24\times23\times\dots\times17}{8\times7\times\dots\times1} \times \frac{18\times17\times16}{3\times2\times1}}{\frac{42\times41\times\dots\times32}{11\times10\times\dots\times1}}\)
\( = \frac{\frac{29654190720}{40320} \times \frac{4896}{6}}{\frac{42\times41\times\dots\times33\times32}{11\times10\times\dots\times1}}\)
To simplify the denominator we could expand the factorials:
\( \frac{42\times41\times\dots\times33\times32}{11\times10\times\dots\times1} = \frac{42\times41\times40\times39\times38\times37\times36\times35\times34\times33\times32}{11\times10\times9\times8\times7\times6\times5\times4\times3\times2\times1}\)
We can make a lot of simplifications.
\(= \frac{\left(7\times6\right)\times41\times\left(10\times4\right)\times39\times\left(2\times19\right)\times37\times\left(9\times4\right)\times\left(5\times7\right)\times34\times\left(11\times3\right)\times\left(8\times4\right)}{11\times10\times9\times8\times7\times6\times5\times4\times3\times2\times1}\)
Crossing out factors in both numerator and denominator, the denominator disappears (reduces to 1), and we are left with:
\( = 41\times39\times19\times37\times4\times7\times34\times4 = 4280561376\)
Plugging this back in we get:
\( p_{sample} = \frac{\frac{29654190720}{40320} \times \frac{4896}{6}}{4280561376}\)
The two fractions in the numerator can also be simplified to:
\( p_{sample} = \frac{735471 \times 816}{4280561376}\)
\( = \frac{600144336}{4280561376}\)
Numerator and denominator are both divisible by 15504 so we get:
\(p_{sample} = \frac{38709}{276094} \approx 0.1402\)
Step 2: Determine the minimum and maximum of the top-left cell.
\(a_{min} = \text{MAX}\left(0, C1 + R1 - n\right)\)
\(= \text{MAX}\left(0, 11 + 24 - 42\right)\)
\(= \text{MAX}\left(0, -7\right)\)
\(= 0\)
For the maximum value of a:
\(a_{max} = \text{MIN}\left(R1, C1\right)\)
\(= \text{MIN}\left(24, 11\right)\)
\(= 11\)
Step 3: Go over all possible values of the top-left cell and calculate the probability. Add it to the p-value if it is less or equal to the one from the sample.
We start with the minimum option of \(a=0\). In that case:
\(b = R1 - a = 24 - 0 = 24\)
\(c = C1 - a = 11 - 0 = 11\)
\(d = R2 - c = 18 - 11 = 7\)
Now we calculate the probability of this arrangement:
\(p_{table} = \frac{\binom{24}{0}\times\binom{18}{11}}{\binom{42}{11}}\)
Note that the denominator is the same, and will be the same for all tables we are going to calculate, so we get:
\(p_{table} = \frac{\binom{24}{0}\times\binom{18}{11}}{4280561376}\)
\( = \frac{\frac{24!}{0!\times\left(24-0\right)!}\times\frac{18!}{11!\times\left(18-11\right)!}}{4280561376}\)
\( = \frac{\frac{24!}{0!\times24!}\times\frac{18!}{11!\times7!}}{4280561376}\)
\( = \frac{\frac{18\times17\times\dots\times12}{7!}}{4280561376}\)
\( = \frac{\frac{18\times17\times16\times15\times14\times13\times12}{7\times6\times5\times4\times3\times2}}{4280561376}\)
\( = \frac{\frac{\left(6\times3\right)\times17\times\left(4\times4\right)\times\left(5\times3\right)\times\left(7\times2\right)\times13\times\left(2\times6\right)}{7\times6\times5\times4\times3\times2}}{4280561376}\)
\( = \frac{17\times4\times3\times2\times13\times6}{4280561376}\)
\( = \frac{31824}{4280561376}\)
\( = \frac{3}{403522} \approx 0.000\)
The next option is \(a=1\). In that case:
\(b = R1 - a = 24 - 1 = 23\)
\(c = C1 - a = 11 - 1 = 10\)
\(d = R2 - c = 18 - 10 = 8\)
Now we calculate the probability of this arrangement:
\(p_{table} = \frac{\binom{24}{1}\times\binom{18}{10}}{\binom{42}{11}}\)
Note that the denominator is the same, and will be the same for all tables we are going to calculate, so we get:
\(p_{table} = \frac{\binom{24}{1}\times\binom{18}{10}}{4280561376}\)
\( = \frac{24\times43758}{4280561376}\)
\( = \frac{99}{403522} \approx 0.0002\)
The next option is \(a=2\). In that case:
\(b = R1 - a = 24 - 2 = 22\)
\(c = C1 - a = 11 - 2 = 9\)
\(d = R2 - c = 18 - 9 = 9\)
Now we calculate the probability of this arrangement:
\(p_{table} = \frac{\binom{24}{2}\times\binom{18}{9}}{\binom{42}{11}}\)
\( = \frac{\binom{24}{2}\times\binom{18}{9}}{4280561376}\)
\( = \frac{276\times48620}{4280561376}\)
\( = \frac{1265}{403522} \approx 0.0031\)
The next option is \(a=3\). In that case:
\(b = R1 - a = 24 - 3 = 21\)
\(c = C1 - a = 11 - 3 = 8\)
\(d = R2 - c = 18 - 8 = 10\)
Now we calculate the probability of this arrangement:
\(p_{table} = \frac{\binom{24}{3}\times\binom{18}{8}}{\binom{42}{11}}\)
\( = \frac{\binom{24}{3}\times\binom{18}{8}}{4280561376}\)
\( = \frac{2024\times43758}{4280561376}\)
\( = \frac{8349}{403522} \approx 0.0207\)
We keep doing this for all values of a until we reach the maximum of 11
a = 4 gives \(\frac{2277}{28823}\approx0.0790\)
a = 5 gives \(\frac{5313}{28823}\approx0.1843\)
a = 6 gives \(\frac{5313}{19721}\approx0.2694\)
a = 7 gives \(\frac{34155}{138047}\approx0.2474\)
a = 8 gives \(\frac{38709}{276094}\approx0.1402\)
a = 9 gives \(\frac{12903}{276094}\approx0.0467\)
a = 10 gives \(\frac{2277}{276094}\approx0.082\)
a = 11 gives \(\frac{23}{39442}\approx0.0006\)
The last thing to do, is add all the found probabilities, for those that were less or equal to the sample. In this example when 'a' is 0, 1, 2, 3, 4, 8, 9, 10 and 11.
\(\frac{3}{403522} + \frac{99}{403522} + \frac{1265}{403522} + \frac{8349}{403522} + \frac{2277}{28823} + \frac{38709}{276094} + \frac{12903}{276094} + \frac{2277}{276094} + \frac{23}{39442} \)
\(=\frac{39}{5245786} + \frac{1287}{5245786} + \frac{16445}{5245786} + \frac{108537}{5245786} + \frac{414414}{5245786} + \frac{735471}{5245786} + \frac{245157}{5245786} + \frac{43263}{5245786} + \frac{3059}{5245786} \)
\(=\frac{1567672}{5245786}=\frac{783836}{2622893} \approx 0.2988 \)
The Fisher Exact Test is quite computational heavy, and for large values this could become a problem. In those cases a Chi-Square test is often used (Pearson or G). The chi-square test can also be used with more than two categories and is discussed in the Nominal vs. Nominal section. There are also specific alternatives for the Fisher test. For example the Barnard test, Boschloo's test, Santner and Snell's test, and Suissa and Shuster's test.
Google adds

