• Home
• Fundamentals
  Introduction What is statistics Terms connected to data Measurement levels Significance SPSS basics
• One variable
  Introduction a binary variable a nominal variable an ordinal variable a scale variable
• Two variables - unpaired
  Introduction binary vs binary binary vs ordinal binary vs scale nominal vs nominal nominal vs ordinal nominal vs scale ordinal vs ordinal ordinal vs scale scale vs scale
• Two variables - paired
  Introduction two nominal two ordinal two scale
• 3+ variables - paired
  Introduction 3+ binary 3+ ordinal 3+ scale
• Distributions
  Introduction Binomial Bivariate Normal Chi-Square (Standard) Normal Student t Wilcoxon (Signed Rank)
• Search

Analysing an ordinal and a scale variable

Part 1: Impression

To begin analysing if there might be differences between different groups on their scores on a scale variable, we might begin by comparing some statistical measurements. Usually I'd recommend to start with a frequency table, which can still be useful, but if the range of the scale variable is very big it might not be very insightful.

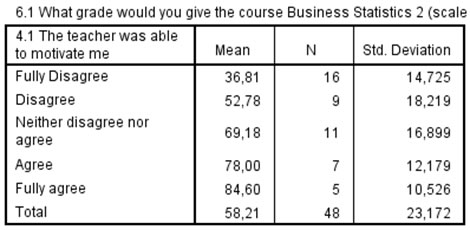
The statistical measures of interest with a scale variable are usually the average (strickly speaking called the arithmetic mean) as a measure to indicate the center, and to indicate a bit about the variation the standard deviation is often reported. For example a course we would like to know if there is a relation between the ability from the teacher to motivate the students (5 point scale fully disagree to fully agree), and the grade students gave for the course (ranging from 0 to 100, with 100 being perfect). Table 1 shows the descriptive measurements.

In the table we see the average (mean). We can see that it seems that the more students agreed with the statement, the higher also the average grade given for the course.

The last column shows something about the variation, measured by something known as the standard deviation. It shows roughly how much each score was above or below the mean. A high standard deviation indicates a high variety in scores, which could indicate that people disagreed with each other, or that something is very unstable. In the example in the highest variation was in the disagree category, it might indicate that some students although they disagreed with the statement, still evaluated the course overall higher.

A visualization might actually be more helpful and easier, which will be discussed on the next page.

Ordinal vs Scale

Introduction

Impression

Visualisation

Test & Effect size

Reporting

Google adds