Distributions
(Standard) Normal Distribution
The APA dictionary of Statistics and Research Methods defines the normal distribution as "a theoretical distribution in which values pile up in the center at the mean and fall off into tails at either end" (Zedeck, p. 238). It often appears in statistics and looks like a bell, but should follow a specific formula (see formula's for the scary looking formula).
Note that not every bell-shape distribution is a normal distribution. The formula requires a mean and standard deviation. However, any normal distribution can be converted to a standard normal distribution.
The standard normal distribution is a specific normal distribution, for which the population mean is fixed as zero, and the sample variance as one. So by substracting the mean and dividing the result by the standard deviation, any normal distribution gets converted to a standard normal distribution. By subtracting the mean and dividing by the standard deviation you get something called a z-score. It tells how many standard deviations something was away from the mean. It gives an indication on how rare a particular score is.
Four examples are shown of a normal distribution in figure 1.
Figure 1Examples of Normal Distribution
Note that the peak of the curve is always at the mean, and the higher the standard deviation, the 'flatter' the bell looks.
As with any continuous distribution it is very important to remember that we are usually only interested in the areas under the curve, since those give us the probability
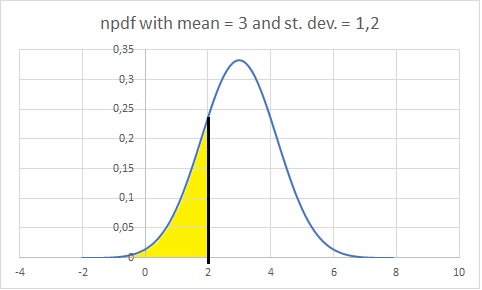
For example the probability of a z-value less than 2, in a normal distribution with a mean of 3 and a standard deviation of 1.2 would be the area highlighted in yellow in figure 2.
Figure 2Example of Area under Normal Distribution
Now calculating this area can be tricky business depending on how easy you want to make it on yourself
Use some software (easy)
Use tables (old school)
Before computers we often made use of tables, like the one shown in figure 3.
Figure 2Cumulative Standard Normal Distribution Table
To illustrate how to use this, let's imagine we had a z-value of -0.53, and want to know the probability of having a z-value of -0.53 or less (assuming a normal distribution)
First you notice all the values are positive, so how can we find -0.53? Well, the standard normal distribution is symmetrical around the center which is at 0. The area under the curve for -0.53 or less, is the same as the area under the curve for 0.53 or more.
Great, so we just look up 0.53? Nope, because now we need 0.53 or more, while the table will only show us 0.53 or less. Luckily the total area under the curve should be 1, so what we could do is determine the probability for a z-value of 0.53 or less, and then subtract this from 1.
To find this probability we look for the integer and first decimal in the first column, in this example 0.5. Then look in that row at the column which has the second decimal, in the example the 0.03. This is highlighted in figure 3
Figure 3Cumulative Standard Normal Distribution Table Example
We find the value of 0.70194. That is the probability for a z-value of 0.53 or less. After we subtract this from 1, we get 1 - 0.70194 = 0.29806, as the probability of a z-value of -0.53 or less.
You might wonder if we should have excluded 0.53 itself, but for a continuous distribution the probability for exactly a z-value of 0.53 or any z-value will be next to 0 (1 / infinity), so no we don't need to worry about that.
With statistical tests we often need the probability of an event or even more extreme. This means an event as likely or even less likely than a z-value of -0.53. This is therefor also a z-value of 0.53 or more. Since the distribution is symmetrical we can simply double the one-sided -0.53 probability we found and get 2 times 0.29806 = 0.59612.
Do the math (hard core)
\( npdf\left(x, \mu, \sigma\right) = \frac{1}{\sigma\times\sqrt{2\times\pi}}\times e^{-\frac{1}{2}\times\left(\frac{x-\mu}{\sigma}\right)^2} \)
If the mean \( \mu \) is equal to 0, and the standard deviation \(\sigma\) equal to 1 we can simplify this a little
\( snpdf\left(z\right) = \frac{1}{1\times\sqrt{2\times\pi}}\times e^{-\frac{1}{2}\times\left(\frac{z-0}{1}\right)^2} \)
\( = \frac{1}{\sqrt{2\times\pi}}\times e^{-\frac{1}{2}\times z^2} \)
Which is the formula for the standard normal distribution probability density function.
To calculate the areas underneath the curve for less than z, we can use the integral
\( sncdf\left(z\right) = \int_{x=|Z|}^{\infty}\left(\frac{1}{\sqrt{2\times\pi}}\times e^{-\frac{z^2}{2}}\right) \)
Use Bars to approximate
One way to calculate this integral is to split the area in small rectangles, and use the npdf to calculate the height
Let's say we wanted to calculate the probability of a z-value of -0.53 or less. Now since the normal distribution is symmetrical, we know that the probability of a z-value of 0 or less is 0.5. If we subtract the probability of a z-value between -0.53 and 0 from this, we should get our desired result
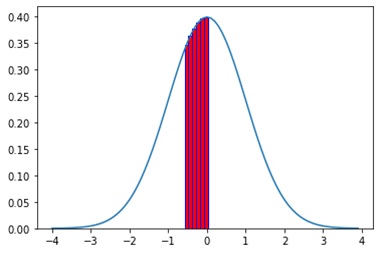
We start with placing a very thin vertical bar at -0.53 with a width of only 0.03, and the height equal to npdf(-0.53), then a small vertical bar from -0.50 to -0.40 (a widht of 0.1) with a height of npdf(-0.50), a bar from -0.40 to -0.30 with height npdf(-0.40), a bar from -0.30 to -0.20 with height npdf(-0.30), a bar from -0.20 to -0.10 with height npdf(-0.20), and finally one from -0.10 to 0 with height npdf(-0.10). This is illustrated in figure 4.
Figure 3Normal Integral Calculation
So the first bar will have a height of:
\( snpdf\left(-0.53\right) = \frac{1}{\sqrt{2\times\pi}}\times e^{-\frac{1}{2}\times \left(-0.53\right)^2} \approx 0.3467 \)
Since the width of this first bar is 0.03, the area of this bar will be 0.03 × 0.3467 \(\approx\) 0.0104
For the second bar we get as height:
\( snpdf\left(-0.5\right) = \frac{1}{\sqrt{2\times\pi}}\times e^{-\frac{1}{2}\times \left(-0.5\right)^2} \approx 0.3521\)
Which has a width of 0.10, so an area of 0.10 × 0.3521 \(\approx\) 0.0352
The calculations for the other bars:
\( 0.10\times snpdf\left(-0.4\right) = \frac{1}{\sqrt{2\times\pi}}\times e^{-\frac{1}{2}\times \left(-0.4\right)^2} \approx 0.10\times 0.3683 \approx 0.0368\)
\( 0.10\times snpdf\left(-0.3\right) = \frac{1}{\sqrt{2\times\pi}}\times e^{-\frac{1}{2}\times \left(-0.3\right)^2} \approx 0.10\times 0.3814 \approx 0.0381\)
\( 0.10\times snpdf\left(-0.2\right) = \frac{1}{\sqrt{2\times\pi}}\times e^{-\frac{1}{2}\times \left(-0.2\right)^2} \approx 0.10\times 0.3910 \approx 0.0391\)
\( 0.10\times snpdf\left(-0.1\right) = \frac{1}{\sqrt{2\times\pi}}\times e^{-\frac{1}{2}\times \left(-0.1\right)^2} \approx 0.10\times 0.3970 \approx 0.0397\)
Now we add them all up to get: 0.0104 + 0.0352 + 0.0368 + 0.0381 + 0.0391 + 0.0397 = 0.1993. So this is the very rough approximate probability of a z-value between -0.53 and 0. But wait...we needed to subtract this from 0.5, which gives: 0.5 - 0.1993 = 0.3007. So this is our estimate for the probability of a z-value of -0.53 or less.
The actual probability would actually be closer to 0.2981 but this was just as an illustration. You can get better approximations by creating more bars with thinner widths, and/or use a trapezium at the end, but hope this example was good enough to get the idea.
Numerical approximation
There are also numerical approximations possible. Three variations:
ACM Algorithm 209
An algorithm by Ibbetson (1963) is shown in figure 4
Figure 4ACM Algorithm 209
As an example, let's say we wanted to determine the probability for a z-value of -0.53 or less
The z-value is not 0, so we move to the right and set:
\( y=\frac{\left|-0.53\right|}{2} = \frac{0.53}{2} = 0.265 \)
Since y is not greater or equal to 3, we move to the right in the flow chart.
Since 0.265 is less than 1 we go down in the flow chart and set:
\( w = y^2 = 0.265^2 \approx 0.0702 \)
\( pVal = \left(\left(\left(\left(\left(\left(\left(\left(0.000124818987\times0.0702 - 0.001075204047\right)\times0.0702 + 0.005198775019\right)\times0.0702 - 0.019198292004\right)\times0.0702 + 0.059054035642\right)\times0.0702 - 0.151968751364\right)\times0.0702 + 0.319152932694\right)\times0.0702 - 0.531923007300\right)\times0.0702 + 0.797884560593\right)\times0.265\times2 \)
\( \approx 0.4039 \)
Next in the flow chart we see that the z-value is not above 0, so we move to the right and:
\( pVal = \frac{1 - pVal}{2} = \frac{1 - 0.4039}{2} = \frac{0.5961}{2}= 0.29805 \)
The result with Excel would have been 0.2981, so this algorithm was off by only 0.05. If I hadn't used rounded values in the calculations, it would have been even closer with 10 decimal places correct.
Algorithm 26.2.17
An Algorithm from Hart (1968, p. 932) is as follows
Set the following values:
- b0 = 0.2316419
- b1 = 0.319381530
- b2 = -0.356563782
- b3 = 1.781477937
- b4 = -1.821255978
- b5 = 1.330274429
Then calculate:
\( t = \frac{1}{1+b0\times z}\)
And finally
\( p = 1-snpdf\left(z\right) \times \sum_{i=1}^5 b_i\times t^i \)
So to determine the probability for a z-value of -0.53 or less, we use:
\( t = \frac{1}{1+0.2316419\times -0.53} \approx 1.14\)
\( p = 1-snpdf\left(-0.53\right) \times \sum_{i=1}^5 b_i\times t^i \)
\( = 1-snpdf\left(-0.53\right) \times \left(b_1\times t + b_2\times t^2 + b_3\times t^3 + b_4\times t^4 + b_5\times t^5\right) \)
\( = 1-snpdf\left(-0.53\right) \times \left(0.319381530\times 1.14 + -0.356563782\times 1.14^2 + 1.781477937\times 1.14^3 + -1.821255978\times 1.14^4 + 1.330274429\times 1.14^5\right) \)
\( = 1-snpdf\left(-0.53\right) \times 2.2053 \)
The snpdf\left(-0.53\right) can be calculated as well:
\( snpdf\left(-0.53\right) = \frac{1}{\sqrt{2\times\pi}}\times e^{-\frac{1}{2}\times \left(-0.53\right)^2} \approx 0.3467\)
So finally:
\( p = 1-0.3467 \times 2.2053 \approx 1 - 0.7022 = 0.2978 \)
The result with Excel would have been 0.2981, so this algorithm was off by only 0.003. If I hadn't used rounded values in the calculations, it would have been even closer with 0.29799
West Algorithm
An algorithm by West (2004) is shown in figure 5
Figure 4West Algorithm
As an example, let's say we wanted to determine the probability for a z-value of -0.53 or less
First we set:
\( zAbs = \left|z\right| = \left|-0.53\right| = 0.53 \)
Since 0.53 is not greater than 37 we move to the right and set:
\( pwr = e^{-\frac{zAbs^2}{2}} = e^{-\frac{0.53^2}{2}} \approx 0.8690 \)
Next we determine that 0.53 is less than 7.071...so we move down and calculate:
\( bld = \left(\left(\left(\left(\left(b0 + b1\times zAbs\right)\times zAbs + b2\right)\times zAbs +b3\right)\times zAbs + b4\right)\times zAbs + b5\right)\times zAbs + b6 \)
\( bld = \left(\left(\left(\left(\left(0.700383064443688 + 0.0352624965998911\times 0.53\right)\times 0.53 + 6.37396220353165\right)\times 0.53 +33.912866078383\right)\times 0.53 + 112.079291497871\right) \times 0.53 + 221.213596169931\right)\times 0.53 + 220.206867912376 \)
\( \approx 374.52\)
\( pVal = pwr\times bld = 0.8690 \times 374.52 \approx 325.4535 \)
\( bld = \left(\left(\left(\left(\left(\left(b0 + b1\times zAbs\right)\times zAbs + b2\right)\times zAbs +b3\right)\times zAbs + b4\right)\times zAbs + b5\right)\times zAbs + b6\right)\times zAbs + b7 \)
\( = \left(\left(\left(\left(\left(\left(1.75566716318264 + 0.0883883476483184\times 0.53\right)\times 0.53 + 16.064177579207\right)\times 0.53 +86.7807322029461\right)\times 0.53 + 296.564248779674\right)\times 0.53 + 637.333633378831\right)\times 0.53 + 793.826512519948\right)\times 0.53 + 440.413735824752\)
\( \approx 0.2981 \)
\( pVal = \frac{pVal}{bld} = \frac{325.4535}{0.2981} \approx 0.2981 \)
Since the z-value of -0.53 is not greater than 0, we are done and the probability is 0.2981.
This matches the result if we had used Excel's formula and if we hadn't rounded it would fully match all decimals, although Excel's decimal expansion is also limited to 15.
Google adds