Ordinal vs Ordinal paired
Part 3a: Test
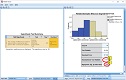
On the previous pages we noticed that before seeing the commercial the scores were fairly evenly distributed among the categories, but after the commercial the first category seems to have a relatively high amount of cases. This was all based on the sample data, but would this also be the case in the population?
Two tests are often mentioned that can be used for this. Either a two-sample sign test, or a Wilcoxon signed rank test (Wilcoxon, 1945). In both tests the difference between the two variables for each case (respondent) is calculated first. The two-sample sign test then 'simply' checks if the number of positive differences is the same as the number of negative differences (or at least could be in the population). This test ignores the size of the difference, and this is something the Wilcoxon signed rank test does take into consideration to a certain extend. As the name implies it uses ranks to determine if the sum of the ranks is significantly different between the sum of the ranks of the positive differences and of the ranks of the negative differences. I'll use this test for the example.
Note that the Wilcoxon test actually removes any ties, i.e. if the score on each variable is the same for a case, it will not be used. Pratt (1959) proposed an alternative method, that does still use these tied scores in the ranking, but it a lot less known. Another approach might be an partially overlapping samples t-test (Derrick & White, 2018), but although this test might actually be the best to use, this would require to make some more assumptions about the data and is not well-known (yet).
In the example there is a significance (p value) of 0.000. This means that there is less than .001 (0.1%) chance to get an absolute Z value of 4.25 or even more in a sample if it would be 0 in the population. This chance is so low that most likely the Z will also not be 0 in the population, which indicates that there is a significant difference between the two variables.
When reading the output/result a few things to look out for. It is important to check how the differences were calculated. In the example this could be either as:
difference A =
before - after, or
difference B =
after - before.
The Wilcoxon signed rank test sums the differences that are positive, and also sums the differences that are negative. If nothing else is stated (as for example in the new method of SPSS) a positive z-value would simply indicate that the first variable had a higher sum (so with difference A the before then scores higher, and with difference B, after scores higher), while a negative z-value would indicate that the second variable had a higher sum (so with difference A the after then scores higher, and with difference B, before scores higher). However some output use the lowest of the two sums (as for example with the Legacy method in SPSS). In those cases you need to check if the positive or negative ranks were used. If the positive ranks were used the interpertation goes the same as mentioned before, but if the negative sum was used everything flips around.
In the example the scores on before were higher. In the example the variables were coded as 1 = fully dislike to 5 = Fully like. A higher value therefor in this example means like it more. We can now be sure to interpret the results as that before seeing the commercial people liked the brand significantly more. Together with the median (see Impression part on how to obtain these) we could write something like:
A Wilcoxon Signed-ranks test indicated people tend to like the brand more before seeing the commercial (Mdn = 3) than after seeing it (Mdn = 2), Z = 4.25, p < .001.
Click here to see how to perform a Wilcoxon signed rank test with SPSS, R (studio), Excel, Python, or Manually
with SPSS
Two methods with the same results to perform this test in SPSS. Note that these videos use a different example
with Excel
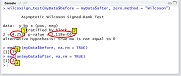
with Python
Manually (formulas and example)
Formulas
In these formulas:
ri is the rank of score i based on absolute differences between two scores, only if they are not equal.
nr is the number of ranks.
ti is the number of tied ranks for the i-th unique rank
u is the number of unique ranks.
Example
Note: different example than in the rest in this section.
We are given the following data with paired results:
Since the 6th pair is missing one entry, it has to be removed. Also pairs that are equal (i.e. the (2,2)) will have to be removed:
The first element shows that this respondent scored a 1 on the first variable, and a 2 on the second.
To determine the ranks we need to determine the absolute difference for each pair, and also remember if it was a positive or negative difference:
The lowest difference is a 1, but we have three of those. So these get rank 1, 2, and 3, or better on average a rank of 2. Then there are two 3's, so rank 4 and 5, or on average 4.5.
The ranks are therefor:
W+ is the sum of the ranks that have a positive sign, and W- the sum of those that had a negative sign:
We have five ranks so:
Therefor:
And
The unique ranks we have are 2, and 4.5. The first occurs three times, the second twice. So for the ties we get:
Then the adjusted variance:
The adjusted standard error is:
Finally the z-value:
As a finishing touch we should also report an effect size measure. This is discussed in the next section.
Google adds